geometry-of-truth

The Geometry of Truth: Dataexplorer

This page contains interactive charts for exploring how large language models represent truth. It accompanies the paper The Geometry of Truth: Emergent Linear Structure in Large Language Model Representations of True/False Datasets by Samuel Marks and Max Tegmark.

To produce these visualizations, we first extract LLaMA-13B representations of factual statements. These representations live in a 5120-dimensional space, far too high-dimensional for us to picture, so we use PCA to select the two directions of greatest variation for the data. This allows us to produce 2-dimensional pictures of 5120-dimensional data. See this footnote for more details.1

Basic datasets

Let’s start off with our basic datasets, containing simple statements like “The city of Beijing is in China” (true) or “Fifty-eight is larger than sixty-one” (false). Mouse over the points below to see which statements they correspond to.

We’re not sure why the smaller_than dataset doesn’t look as separated as the rest. But things look better when you go to 3D (below, right).

Even with these simple plots, there’s already lots to explore! For instance, for larger_than, we see two axes of variation: one separating the red and blue clouds, and one running parallel to the point clouds (pointing up and to the right). Can you figure out what this second axis of variation is? See below for the answer.

Negations

Now let’s introduce some more complicated logical structure to our statements. We’ll start by negating statements by adding the word “not.”

How do the visually apparent “truth directions” of the negated statements compare to the “truth directions” of the un-negated statements? Let’s check:

Here we’ve done PCA on the two datsets together1. You can toggle which datasets are shown by clicking on the plot legends.

What’s going on here? There are many possibilities, but our best guess is what we call the Misalignment from Correlational Inconsistency (MCI) hypothesis. In brief, MCI posits the existence of a confounding feature2 which is correlated with truth on cities and anti-correlated with truth on neg_cities. See our paper for much more discussion .

Conjunctions and disjunctions

Now let’s try some logical conjunctions and disjunctions. Mouse over the datapoints below to see what our conjunctive/disjunctive statements look like.

Does it look like the circled points form a bit of a separate cluster? We thought so, and indeed there’s a pattern to those statements. See if you can figure out what it is (answer below).

Emergence over layers

So far, we’ve only been looking at layer 12. But by sweeping over the layers of LLaMA-13B, we can watch as the features which distinguish true statements from false ones emerge. Interestingly, there’s a 4-layer offset between when cities separates and when cities_cities_conj (conjunctions of statements about cities) separates. This might be due to LLaMA-13B hierarchically building up concepts, with more composite concepts taking longer to emerge.

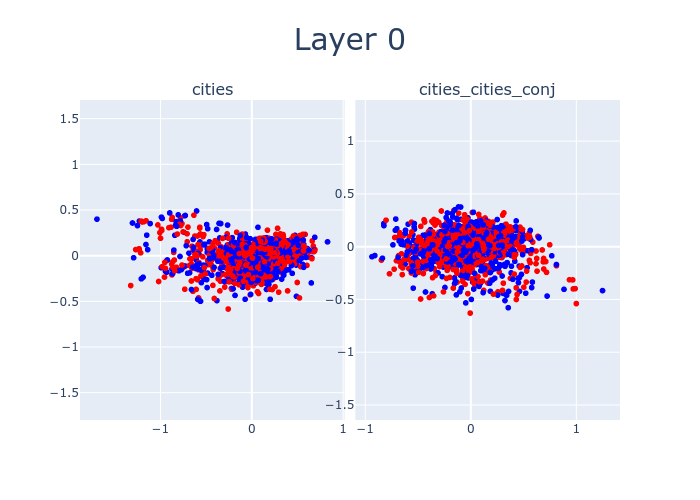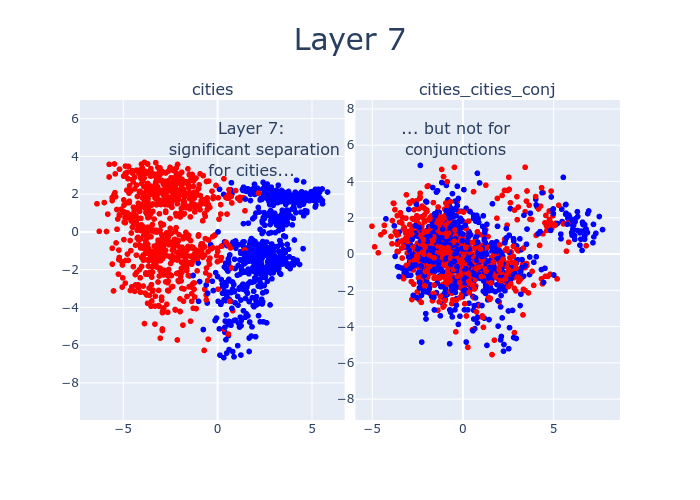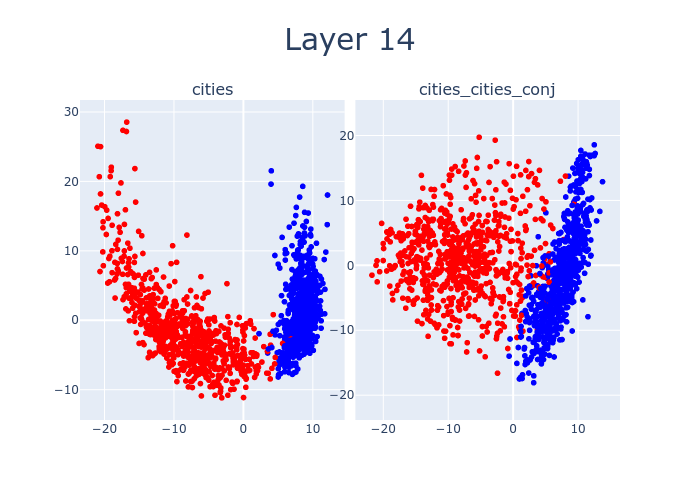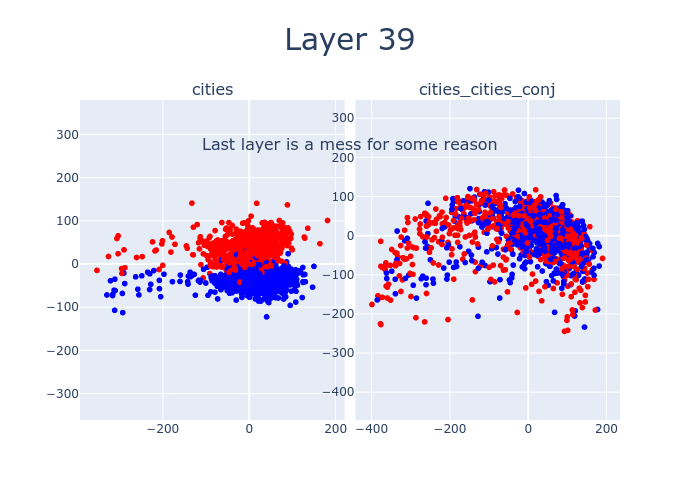
Here’s an interactive version of the above with different datasets.

Interestingly, cities and neg_cities start off antipodally aligned before rotating to be orthogonal like in the plot above (toggle the datasets in the left plot on and off to see this).

More diverse datasets

All of the datasets so far were curated to contain statements which are uncontroversial, unambiguous, and simple. They are also not very diverse – each dataset is formed from a single template.

In contrast, we’ll now look at some uncurated datasets adapted from other sources. Mouse over the plots below to see some of these datasets’ statements.

Why aren’t these datsets separating into true/false clusters? Because of the additional diversity. Recall that PCA identifies the most salient axes of variation for a dataset. In more diverse datasets, these axes are more likely to encode some truth-independent feature. For instance, the statements in companies_true_false are formed using three different templates, and the top 2 principal components mostly encode the difference between these templates. It’s quite shocking that common_claim_true_false, consisting of statements as diverse as “Rabbits can partially digest memories” (false) or “Dolphins are capable of acts of impressive intelligence” (true) has as much true/false separation as it does!

If we want to see separation into true/false clusters, we can borrow one of the PCA bases identified from our cleaner datasets. For instance, here are our uncurated datasets visualized in the PCA basis extracted from our cities dataset.

Other tidbits

We’ve been mainly focusing on truth/falsehood, but there’s also more information present in the representations shown here. For instance, we asked above what the non-truth axis of variation is for our larger_than dataset. Seemingly, for a statement like “x is larger than y,” it represents the absolute value of the difference x - y!3

We also noted a separated cluster for cities_cities_conj, and challenged readers to figure out what distinguishes this cluster. Looking at a few examples, we see that statements involving China and India are common in this cluster. Perhaps it is the China/India cluster? A reasonable first guess, but not quite! Here are some example statements from the cluster:

It seems to be that this cluster is for statements where the country in both halves of the conjunction are the same!4

  1. In more detail, we extract LLaMA-13B residual stream representations over the final token of each statement. (Note that our statements always end with a period.) We center each dataset by subtracting off the mean representation vector; when multiple datasets are involved (e.g. as with cities and neg_cities in the negations section), we center the representations for each dataset independently; if we hadn’t done this, there would be a translational displacement between the two datasets. ↩ ↩2

  2. For instance, this other feature might encode the relation “is in the country of”. With unnegated statements like “The city of Beijing is in China,” this feature correlates with being true; for negated statements like “The city of Paris is not in France” this feature anti-correlates with truth. ↩

  3. In particular, this means that the true and false “close comparisons” are no less separated than the true and false “clear comparisons” – they just appear on the right side of their respective clusters! This was surprising to us. ↩

  4. Since China and India are the countries appearing the most in our cities dataset, the vast majority of the statements which have both countries match are about China and India. ↩